XIAOZHONGMING

来源：同济大学汽车学院  作者：余卓平 夏新 熊璐 曲彤

      摘要：基于分布式驱动电动汽车，提出了一种纵向车速非线性自适应估计算法．该算法使用车辆加速度传感器信息和各车轮滑移率反馈值对车辆纵向车速进行估计．从理论上证明了纵向速度估计误差收敛．根据各车轮滑移率的大小确定各轮速估计误差在估计算法中的反馈修正比例．使用带遗忘因子的递推最小二乘算法在坡道路面对路面坡度进行了在线实时估计，进而使用坡度估计值修正纵向加速度传感器信息，实现了坡度自适应纵向车速估计．该方法具有计算量小、估计精度高的优点．通过多工况的实车试验验证了算法的有效性．


      关键词：分布式驱动电动汽车；非线性估计；坡度自适应；车速估计


      分布式驱动电动汽车动力学控制近年来成为研究热点．纵向车速是进行车辆动力学控制的关键状态之一．分布式驱动电动汽车没有非驱动轮，传统车辆所用的以非驱动轮还原车速的方法不再适用，因此纵向车速估计成为难点．当前国内外学者针对纵向车速估计提出了诸多算法，主要分为两类：运动学方法和动力学方法．


      运动学估计方法主要有以下几种．齐志权等[1]分析了最大轮速法、斜率法、综合法等传统的纵向车速估计方法，然后提出采用递推法来估计纵向车速，并通过最大轮速法和测速雷达采集的与前车的相对车速来修正估计出的车速，以免估计发散．刘国福等[2]利用轮速信号和车身加速度信号，考虑制动过程中车轮半径的变化和加速度传感器的偏移误差，应用递推最小二乘算法实现了车速的实时估计．


      Gustafsson等[3]和Kobayashik等[41采用轮速信号和纵向加速度信号，并根据车辆当前行驶状态来判断信号的可信度，调整权重系数的大小，对车辆的纵向车速进行融合计算．Gao等[5]使用卡尔曼滤波对传感器信息进行融合，并且其考虑了坡度对传感器信号的影响，实现坡度自适应的纵向车速估计．以上基于运动学模型的观测器，鲁棒性较好，估计结果几乎不受模型参数的影响，但估计精度依赖于传感器的信息．


      基于动力学的估计方法核心是估计轮胎的纵向力，而估计纵向力有基于轮胎模型的方法和基于车轮动力学模型的纵向力估计[6]，该方法需要知道轮胎的驱动转矩／制动转矩，对于传统车辆的稳定性控制系统而言，即需要知道发动机输出转矩以及制动器制动转矩[7]．基于动力学模型的观测器，对传感器的要求相对较低，但对模型参数的敏感度较高，鲁棒性不如运动学方法，因此对估计算法提出了更高的要求．


      本文利用分布式驱动电动汽车车轮驱动力信息可精确获取的特点，首先融合运动学和动力学纵向车速估计方法，设计了一种新的非线性纵向车速估计算法．该方法使用车辆纵向加速度传感器信息和各个车轮的轮速估计误差的反馈对纵向车速进行估计．其次在理论上对纵向车速估计误差进行了分析，并进行了其收敛性证明．然后使用带遗忘因子的递推最小二乘算法对路面坡度进行估计，以矫正车速估计算法中所使用的加速度信息来实现算法的坡度自适应．最后，在水平路面上进行了多组实车试验，包括不同附着系数条件下的直线加(减)速工况和高附着系数的蛇形、双移线和方向盘角阶跃输人工况，以及坡道路面的直线加减速工况，通过对试验结果进行分析，验证了本文提出纵向估计算法的有效性．


      1. 纵向车速估计算法

      1．1车速估计原理











      1．2估计误差分析











      由以上误差收敛证明可见，在轮胎纵滑特性曲线斜率大于零段，估计算法总能保证估计误差收敛到某一值或其以下．在某些恶劣工况，当轮胎工作于纵滑特性曲线斜率小于零段时，应结合车轮的滑移率控制将轮胎的工作点维持在斜率大于零部分，一方面可以准确估计出纵向车速，另一方面可以较大限度地利用路面附着力．


     1．3车速估计的坡度自适应


      根据式(1)可得，为准确获知车速，需使用加速度传感器信号值．而加速度传感器信号值包含路面坡度信息，在纵向车速估计中需对其进行修正，因此准确估计出路面坡度是实现纵向车速自适应估计的基础．本文采用运动学与动力学估计相结合的路面坡度估计算法．











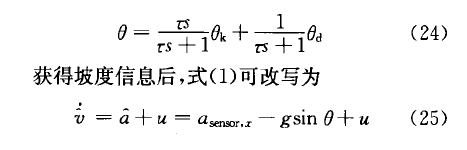
      2.试验与分析


      为验证上文算法的有效性，在水平路面进行了纯纵向运动多工况、带侧向运动多工况以及坡道路面的纯纵向运动工况的试验验证，并且对算法估计相对误差进行了分析．误差分析时，相对误差定义为





      2．1道路试验系统


      试验车基于上汽荣威E50改装，如图l所示．试验车后两轮为轮毂电机驱动，前两轮为轮边电机加减速机构组成的动力总成，主要参数见表1和表2．车辆传感器系统配置如图2所示，试验平台的试验测试系统主要包括：惯性和GPS测量系统、测力方向盘(可提供方向盘转角、转矩信息)、横摆角速度传感器、纵侧向加速度传感器、车辆HGT(加速踏板信号、制动踏板信号、EPs方向盘转角信号)、电机转矩及转速信号(电机控制器提供)、MicroAutoBOx和笔记本电脑．基于该传感器系统，本文提出了非线性自适应纵向车速估计算法．通过访问试验车的CAN总线获得4个电机上传的电机转矩及转速信号，纵向加速度信号由加速度传感器获得，真实纵向车速由GPS惯性导航仪获得．试验场地选取为同济大学新能源汽车工程中心圆形试验场，低附着系数瓷砖路面，中低附着系数湿草坪路面，以及坡道路面．

      2．2水平路面纵向车速估计


      基于试验车利用同济大学新能源汽车工程中心圆形试车场的场地进行了水平路面的试验．直线行驶试验模拟了常规以及越野的工况试验．常规工况试验包括：高附干燥沥青路面直线加减速试验，低附湿瓷砖路面直线加减速试验．越野工况试验包括：中附湿草坪路面直线加减速试验，对接路面直线加速

表l试验车整车参数

表2试验车电机参数

试验．带侧向运动工况包括：高附蛇形试验，高附双移线试验，高附方向盘角阶跃输入试验．以下给出了所有试验的纵向车速估计结果，见图3～10．


      2．2．1纯纵向工况车速估计


      由于低速起步阶段轮速传感器测量信号有效值较小，噪声相对较大．因此低速起步阶段，当车速小于3 m·s_1时，误差分析采用绝对误差．当车速大于3 m·s_1时，采用相对误差进行分析．

      水平路面直线加减速工况实车试验车速估计结果如图4、图6、图8和图10所示．试验结果误差分析结果见表3．图4、图8为估计算法在乘用车较多见的常规情况下的估计结果，在高附着系数干燥沥青路面与低附着系数湿瓷砖路面直线加减速工况下，算法的估计相对误差在2．5％以内，并且随着车速的提高，估计的绝对误差并没有增大，相对误差进

图4高附干燥沥青路面直线加减速纵向车速估计结果

图5 中附湿草坪路面直线加减速工况加速度

图6 中附湿草坪路面直线加减速纵向车速估计结果

      一步减小，能够准确地估计出纵向车速．图6、图10为估计算法在乘用车较少见的越野情况下的估计结果，在中低附着系数的湿草坪路面与高低附着系数

图7低附湿瓷砖路面直线加减速工况加速度

图8低附湿瓷砖路面直线加减速纵向车速估计结果

图9对接路面直线加速工况加速度

      对接路面的直线加减速工况下，较常规情况，估计的相对误差有所增大但仍然能够保持在7％以内，并且绝对误差在o．25 m·s_1以内．在图10所示的对接路面上，可以看到在3．6 s时，估计的相对误差较大，这是由于附着系数变化，导致了车轮滑移率估计误

图10对接路面直线加速纵向车速估计结果

差，进而影响了其在公式(1)中的修正项“，但是随着时间的推移，估计误差能够迅速收敛到较小值，与理论证明误差收敛保持一致．对于这种情况，应结合滑移率控制将车轮控制在纵向线性特性范围之内来减小估计误差．无论在常规路面还是越野路面，算法始终能够保证估计误差的收敛，精度能够满足要求．2．2．2带侧向运动工况的车速估计在国标GB／T 6323．1—94对蛇形工况要求的基础上，根据试验场地条件和车辆性能，设计并进行图11所示短桩距蛇形试验．实验工况及结果如图12，13所示．

      在IS03888标准对双移线工况要求的基础上，根据试验场地条件和车辆性能，设计并进行图1 4所示短桩距双移线试验．实验工况及结果如图15，16所示．


      高附方向盘角阶跃输人工况及结果如图17，18所示．


      图13、图16以及图18为算法在高附着系数路面极限工况下的估计结果．相比于常规路面下直线加减速工况，带侧向运动工况的估计相对误差有所增大，蛇形工况最大估计误差为4．1％，双移线工况最大估计误差为3．8％，方向盘角阶跃输人工况下估计误差为3．5％．但是仍然能够收敛在4．1％以内．在带侧向运动的极限工况中，轮胎易进人侧偏特性的非线性区域，由于轮胎的纵侧向特性的耦合现象，较大侧偏影响了其纵向特性，这导致了式(8)中所使

图12高附蛇形工况介绍

图13高附蛇形纵向车速估计结果

用的轮胎纵向特性模型略微有所摄动，进而影响滑移率估计结果的精度，而由式(9)，式(10)可知，滑移率的估计精度影响式(1)中的修正项“的值．因此在

图15高附双移线工况介绍

图16高附双移线纵向车速估计结果

      带侧向运动的极限工况下，算法的估计相对误差略微有所增大，但仍然能够保证收敛．通过表4对误差的分析，也验证了算法在极限工况下的鲁棒性．表明了算法在复杂极限工况条件下的适用性．

表4带侧向运动工况估计误差

以上通过水平路面的纵向行驶工况与带侧向运动的行驶工况的实车试验，验证了算法的有效性与其在理论上对于误差收敛的证明．

图17高附方向盘角阶跃输入工况介绍

图18高附方向盘角阶跃输入纵向车速估计结果

      2．3坡道路面纵向车速自适应估计


      由于试验条件限制，利用同济大学新能源汽车工程中心实验室外地面至二楼的上坡(实际情况如图19所示)，进行了坡道直线行驶工况的纵向车速自适应估计试验验证．试验过程为上坡前的平地起步，进而变油门安全上坡，最后在二楼实验室门前的平台处减速停车．对坡度的估计结果如图20所示，估计该坡度角为6。左右．纵向车速估计试验结果如图21所示．

      如图21所示，直接利用车载加速度传感器信息估计车速，会造成明显的偏差，估计误差在10％左右．在准确的坡度估计的基础上，纵向车速估计所需要的纵向加速度信息得以修正，使得纵向车速估计结果更加准确，通过坡度的估计对纵向车速估计进行自适应矫正之后，估计误差能够明显减小．而相比于平面道路上的准确估计，尚存在的误差主要在于上坡道路上车身的俯仰对纵向加速度信息的影响验证了在坡道路面的纵向车速自适应估计的有效性．


      3 结论


      本文研究了分布式驱动电动汽车纵向车速的估计问题，设计了一种非线性自适应纵向车速估计器，并进行了实车试验，得出以下结论：


      (1)提出了一种非线性纵向车速自适应估计方法．根据各车轮滑移率的大小确定其轮速估计误差在估计算法中的反馈修正比例，结合加速度传感器信号对纵向车速进行估计．多工况的实车试验表明，在轮胎纵滑特性斜率大于零的范围内估计能够保持高精度．侧向滑移对算法的影响较小．在某些工况下，轮胎纵向特型可能进入到纵滑特性斜率为负的区域，导致估计误差略微增加，对于这一现象，可以结合车轮的滑移率控制将轮胎的纵向滑移保持在线性范围之内，保持较高的估计精度．


      (2)对估计算法的估计误差进行了分析，并根据理论推导证明了误差收敛．并且多工况实车试验验证了估计误差的收敛性．


      (3)在坡道路面采用使用带遗忘因子的最小二乘算法的动力学方法得到的坡度估计值与采用运动学方法得到的坡度估计值进行融合，其结果用于修正纵向加速度传感器信息，实现纵向车速的自适应估计．实车试验结果表明，坡度的自适应估计能够明显改善车速估计精度．