XIAOZHONGMING

  摘要: 从自动化车床连续加工某种零件的故障检测问题出发，探究了检测方法与刀具更新对于生产
附加成本的关系。建立了有更新点的检查维护和预防性刀具更新的检测优化模型; 给出了自动化车
床刀具检测优化模型研究检查成本、不合格零件损失期望和包含故障维护费用与刀具定期更换费用
的总维护费用的期望的计算方法; 得到了以一定检测间隔、预防性刀具更换周期为自变量的平均生
产附加成本函数，取得了较优定期检测间隔和定期刀具更换间隔; 运用蒙特卡洛随机仿真的方法，进
行了仿真模拟，检验了模型结果的优越性。
  
     关键词: 刀具; 更换策略; 检测间隔; 条件概率; 蒙特卡洛模拟

      0 引言
  
     可靠性及维修性策略问题一直受到人们的广泛关注和研究，通过设计系统可靠性及维修性策略，可提高重要产品和复杂工业系统的可靠性和可用性，降低生产成本。自动化车床管理是一个比较复杂的研究课题之一，要保持工序的正常运行，需要经常对工序进行检查。检查周期长，可以减少检查费用，但由于不能及时发现故障会给生产带来损失; 检查周期短，虽然能够及时发现故障少出不合格品，但检查费用高，因此，须找出最佳的检查周期使得工序运行单位时间内的平均损失达到最小。
  
     由于自动化车床运行中产生次品的故障主要为刀具故障，其它故障为小概率事件［1-2］，所以，在只考虑刀具故障的前提下，通过概率论和更新过程理论，建立以单位时间内期望费用为目标函数的数学模型，以检测间隔和刀具更换时刻为策略，确定最优的策略使得工序长期运行单位时间内期望费用达到最小。我们通过模型化的方法及一定的数学手段来求出较优定期检测间隔和定期刀具更换间隔，并寻求是否有更好的检测策略。
  
      1 、问题的基本假设
  
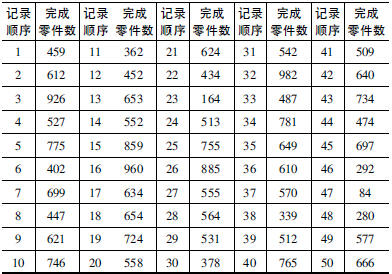
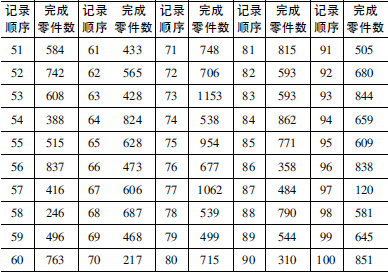
     用自动化车床连续加工某种零件，刀具损坏是出现故障的主要原因。现记录了100 次故障出现时刀具完成的零件数，如表1 所示。
  
     问题1: 假设故障时产出均为不合格的零件，正常时产出均为合格的零件，设计效益最好的检查间隔( 生产多少零件检查一次) 和刀具更换策略。问题2: 如果正常时产出不全是合格的零件，有2%的不合格率; 而故障时产出的零件有40% 为合格率， 60%为不合格率。设计效益最好的检查间隔和刀具更换策略。
  
     问题的基本假设如下:
  
     ( 1) 假设生产每个零件时工序出现故障是完全随机的，且故障完全随机。
     ( 2) 假设生产每个零件时刀具故障仅与刀具寿命有关。
     ( 3) 假设仅能通过检测零件来判断是否出现故障，即故障必须在检查点才能被发现，且无法单纯从一次检验判断该故障是刀具损坏故障还是其他故障。
     ( 4) 假设检测零件过程不会出错，即对零件本身的不合格检测没有误判。
     ( 5) 假设无论是95% 的刀具损坏故障还是5% 的其他故障，发生故障并使其恢复正常的平均费用均为3000 元/次( 包括刀具费用) 。每次恢复正常的过程都
进行刀具更新操作。
     ( 6) 假设问题2 中工序正常时误判为有故障停机产生的费用( 1500 /次) 已包含刀具更换费用，即刀具在误判时被更新。零件时才进行调整，即检查次数的增多不会有更多
误工损失。
  
  
                        表1 100 次刀具故障记录( 完成零件数)

             

      

     2 、问题分析
   
     自动化车床连续加工零件过程中会产生故障，故障后会导致不合格零件产生。通过定期检测零件来检测故障与维修，通过定期更换刀具预防工序故障。过长的检查周期会导致故障不能及时被发现，大量不合格零件被生产，造成损失。过短的检查周期又会造成检查成本过高。类似的，过长的刀具更换周期无法起到很好的预防故障效果，过短的刀具更换周期又会使成本急剧上升。因此，两个关键变量需要统筹兼顾，综合考虑。
   
     此外，问题1 与问题2 需要分别进行分析。问题1 假定工序故障是产出的零件均为不合格品，正常时产出的零件均为合格品。则通过零件合格与否来判断工序故障为完全准确。
  
     问题2 该工序正常时产出的零件不全是合格品，有2%为不合格品; 而工序故障时产出的零件有40%为合格品， 60% 为不合格品。则通过零件合格与否来判断工序故障存在误判风险，需要对误判进行条件概率的计算以准确算出附加成本期望。
  
     综上所述，该题要解决的是一个以单位附加成本最低为目标，检查间隔和换刀间隔为自变量的优化问题［4-5］。

      3 、模型的建立
  
     3． 1 数据处理及故障间隔函数的确定
  
     根据给出的100 个刀具故障记录，采用Matlab 软件进行数据处理，得到散点拟合图，如图1 所示。

  

      

                          图1 刀具故障记录散点拟合图
  
     由图1 可知刀具寿命近似服从正态分布。可假设X 的概率密度函数为

      

     因此，在显著性水平α = 0． 05 下接受总体服从正态分布。根据基本假设，非刀具故障，即其他故障在生产每个零件时的故障概率相同。因此，可得每个零件非刀具故障的概率p 为

  
     
  

     3． 2 基本模型的建立
  
     通过对问题的分析可知，该问题是一个单目标优化问题，其目标函数为零件的平均附加成本F，F 的值越小则方案越优。下面我们就零件平均成本的影响因素进行分析，并建立相应的基本数学模型。
  
     不难发现，整个生产附加成本由三部分组成，即检查费用，不合格零件损失费用以及维护成本，其中维护成本又包含发现故障后的调整成本和定期换刀的预防成本。附加成本示意图，如图2 所示。

      

                            图2 附加成本示意图
   
     3． 2． 1 检查过程
  
     由基本假设可知，检查是通过对零件是否合格的检查来判断，设检查过程是等间隔进行的，间隔为N。显而易见，检查费用= 检验次数× 单次费用，设共生产M 个零件，即有检验费用Et

     

     左右两个节点表示两节点间整段生产过程情况。两节点之间的区域称之为一个区间。
   
      3． 2． 2 不合格零件损失费用
   
     由于检测方式是由零件是否合格来判断，则若某检查点发现零件不合格，则工序故障必定在两个检查点之间。但由于问题2 中存在着工序状况与零件状况不完全一致的概率，因而，问题1 和问题2 的不合格零件损失费用需分别考虑。
  
     问题1: 工序故障时产出的零件均为不合格品，正常时产出的零件均为合格品。则若第k 次检查出现了不合格品，那么工序故障必定发生在第( k － 1) 次检查和第k 次检查之间，即第( k － 1) n 个零件和第kn 个零件之间，如图3 所示。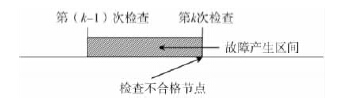

      
                        图3 产生故障情况示意图
   
     将这两个检查点之间的区间放大，可知共有n 个点可能发生工序故障。可以求得不合格零件损失费用Ef。

      

     问题2: 如果该工序正常生产零件不全是合格品，有2%为不合格品; 工序故障时产出零件有40% 的合格品。因此，当第k 次检查检查到不合格时，除去工序正常的误判，工序故障的产生区间可能有不同的情况，除问题1 所示情况外，可能发生如图4 所示的情况。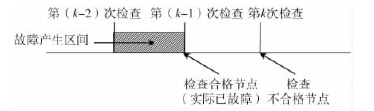

        
                             图4 可能产生故障情况
   
     因此，不合格零件损失费用期望的计算需要进行改进，即

      

      不合格零件由工序故障下产生次品和工序正常下产生次品两部分构成。其中工序故障下产生次品的概率不再是通过问题1 中简单的工序故障区间进行计算，故障产生区间存在条件概率［6-9］。‘

     工序故障记为FG，工序正常记为SG，检查到次品FP，检查到合格品SP。
  
     据贝叶斯公式，有

     

     3． 2． 3 维护成本
   
     维护成本是整个附加成本计算中的重要一环。维护成本包括两个方面，分别为发生故障时调整设备产生的费用及预防性更换刀具所产生的费用。在问题2中，由于认定工序故障存在误判，所以维护成本中还需加入工序正常而误认为有故障停机的损失。
  
     基于以上讨论，维护费用期望值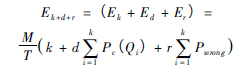

      
  
     其中Ek为预防性换刀的费用期望，Ed为出故障调节的费用期望，Er为误判停机费用期望( 对于问题一，Er = 0) 。该式中Pwrang为条件概率，由计算可知

      
  
     因此，节点换刀概率的递推关系式为:
  
      
  
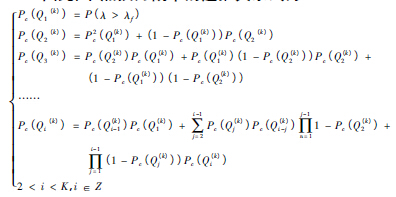
     其中P( λ ＞ λf) 是指此次( 换刀后第一次检查行动) 判定为故障的概率。
  
     检查过程的流程示意图，如图5 所示。

      
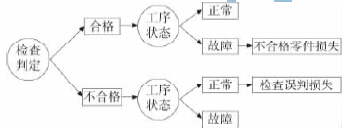
                           图5 检查过程的流程示意图
   

      4 、结果分析
  
      4． 1 模型结果
  
     通过用Matlab 软件对以上算法进行计算机的算法实现，得到了问题1 的结果，如图6 所示，检查间隔18，检查次数19，即预防性换刀周期为342，附加成本4． 890; 问题2 的结果，如图7 所示，检查间隔36，检查次数13，即预防性换刀周期为468，附加成本9． 536。

     

                               图6 问题1 计算结果
   
  

      

                           图7 问题2 计算结果

      从这两个结果发现，虽然问题2 中的检查间隔变长，即检查次数变少，但由于误判的产生，多出了误判成本，因而，单位附加成本显著高于问题1 中的单位附加成本。
  
      4． 2 仿真模拟
   
     为了检测算法的可行性，使用蒙特卡洛方法对问题一的算法进行仿真模拟［10-11］，过程如下:
   
      ( 1) 给定换刀间隔T，检查间隔N，以及生产零件个数M;
      ( 2) 设置连续不换刀生产的零件数S，已生产的零件个数F，生产损失和维护Y;
      ( 3) 从第一个零件开始，产生一个随机数，检测是否满足先前拟合出来的概率，如果满足，则将其之后一直到下一个检查点的零件( 包括检查点) 全部记为次品，并计算损失，计入Y; 如果不满足，则进入下一个零件的生产。
      ( 4) 对于第K 个零件，产生随机数，检测是否满足之前拟合出来的概率，如果满足，就将第K 个到K 之后距离最近的检查点之间的所有零件( 包括检查点)记为次品，计算次品损失计入Y，然后在该检查点处更换刀，将换刀损失计入Y; 如果不满足，计入下一个零件生产，并令连续不换刀生产的零件数S = S + 1。将生产零件个数计入F;
      ( 5) 在检查点处，如果发现连续不换刀生产的零件数S 大于T，则直接不检查，然后换刀，将换刀成本计入Y;
      ( 6) F 大于M 时，停止生产，输出对应的T，N 所产生的费用Y;
      ( 7) 取其它的T，N 值，进行同样的过程。对所有的Y 值进行比较。

      取预防性换刀周期与检查间隔为: ( 350，14 ) ，( 342， 18) ，( 396， 22) ，( 416，26) ，( 342，18) ，( 396，22)仿真模拟对比结果，如图8 所示。

         

                               图8 仿真模拟结果
      
     由图8 可知，在给定的较优间隔处，附加成本在较低成本4． 95 附近，符合之前所设的概率规律。并且得到表2 所示的仿真对比表。仿真模拟的结果证明了算法是具有可行性。
  
  
                                         表2 仿真对比表

        
  
  
      5 、结论
   
      本文依据概率统计知识，建立了有更新点的检查维护和预防性刀具更新的初等概率模型，给出了检查成本、不合格零件损失期望和包含故障维护费用与刀具定期更换费用的总维护费用的期望的计算方法，得到了以一定检测间隔、预防性刀具更换周期为自变量的平均生产附加成本函数。运用Matlab 计算，得到最优解。运用蒙特卡洛随机仿真的方法，进行了仿真模拟，检验了模型结果的优越性。