ZHENGMIAN

　超声振动系统是超声电解复合加工装备的关键组成部分，本文结合超声振动理论，采用ANSYS 对变幅杆进行模态分析和谐响应分析，获得共振频率、位移节点和放大系数等重要参数；对超声振动系统中的变幅杆和工具头进行了分析，经试验验证了变幅杆的振幅放大系数及不同变幅杆对加工速度的影响；最后，通过超声复合加工试验，验证了超声电解复合加工的加工效率高、精度高、表面质量更好。
超声电解复合加工机理
    超声电解复合加工是加工难加工材料的新工艺，是将超声频振动、脉冲电流电解加工等技术有机复合在一起的加工方法[1]。
    超声电解复合加工机理见图1。加工过程中，采用低电压（2~6V）、低浓度钝化电解液（如质量分数为5%的NaNO3 水溶液），由于微电流电解作用，在工件表面产生厚度极薄、强度远低于基体材料的电解钝化膜，可阻止低电流密度电解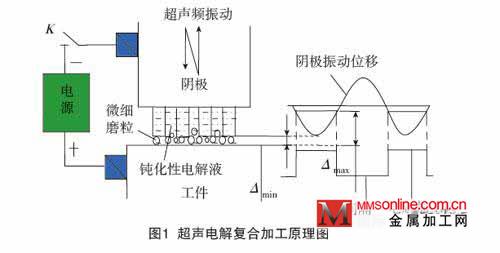

作用。引入超声频振动、脉冲电流，磨粒的冲击刮擦、高频振动冲击波及“负压空化”作用能有效消除钝化膜，及时排除间隙区电解产物，改善及加强电解作用，使加工过程能够连续进行。
　　在微细阴极与工件间由于微细磨粒的存在，存在最小间隙Δ min，约为磨粒最大直径，使阴极与工件避免直接接触，发生电解短路。当阴极与工件间的间隙小于Δ min 时，斩波开关K 闭合，进行电解加工；反之，斩波开关断开，电解作用停止。超声电解复合作用间歇进行，超声效应辅助及时去除电解产物、更新电解液，有利于改善及稳定电解加工间隙状态，提高电解去除定域性，可避免通常大电流密度电解产生的杂散腐蚀作用[2-3]，有效提高加工精度及表面质量，可实现金属导电材料微结构高精度、高效率微细加工。本文采用的是超声电解复合加工的方法，对超声振动系统进行动力学分析后进行微齿轮的加工试验。
超声电解复合加工系统
　　超声电解复合加工装置如图2所示，包括电解装置、超声频振动装置、工作台z 向自动进给及测量装置、电解电流测量分析装置及PC 机控制环节等。电解装置由阴极工具头、微器件及工作液组成。阴极与微器件置于电解液槽中，电解液槽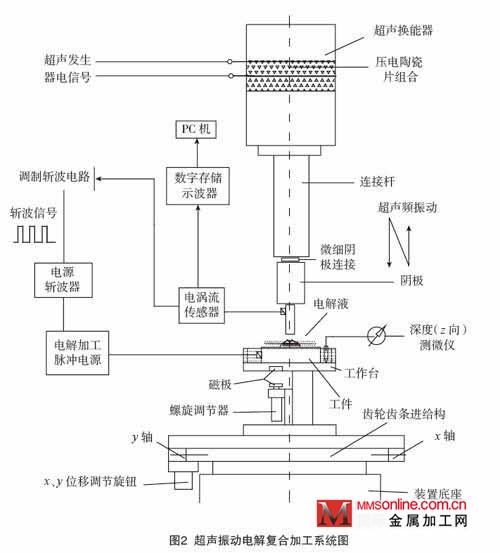

充满静态低浓度钝化电解液，电解电源一端与工具阴极相连，一端与微器件相连。微器件固定在工作台上。工作台可以实现x、y 轴向上的微位移移动，借助测量显微镜可进行阴极与工件的精确位置定位。工具阴极与微器件之间微压力可通过磁悬浮蠕动进给装置实现精确微细调节。工具阴极与微器件之间的间隙随高频振动作周期性变化，微器件加工深度由深度测微仪给出[4]。
　　电解电流测量分析装置由1 个2 Ω 精密电阻、1 台数字存储示波器和1 台PC 微机组成。数字存储示波器的电压信号通过串行口传送到PC 微机中测量、显示、存储，以便进一步优化分析和参数优选控制。
该系统对脉冲电解电源的斩波信号是从超声频信号中取出，通过调制斩波电路对电解电源进行斩波，实现在小间隙时加工，在极小间隙和大间隙时电源关闭（停止加工），从而实现电解电源与超声频振动的同步。
　　电解电源与超声发生器电源之间串入的调制电路将超声发生器产生的超声频交变电信号转换为电解直流（或脉冲）电源的斩波信号，然后传递给电源斩波电路，对电解电源脉冲电压进行适时切断，使电解电压成为与阴极超声频振动保持相位同步的脉冲电压，从而可使电解电源成为与超声波振动同步协调的脉冲电源，相当于超声频振动、脉冲电解复合同步加工，因此可进一步改善电解加工微观过程，提高加工精度[5]。
变幅杆及其动力学分析
　　超声振动系统中的变幅杆主要作用是把机械振动的质点位移或速度放大，或者将超声能量集中在较小的面积上。超声变幅杆的种类很多，常用的有指数形、悬链线形、阶梯形和圆锥形变幅杆。
　　变幅杆设计与研究方法有理论推导、试验研究和数值分析 [6-7]。本文以指数形、圆锥形变幅杆为例，使用有限元软件ANSYS 对其进行相应的分析。与传统的物理学分析相比，有限元分析能够对高精度非线性问题求解，并且具有强大的网格处理能力对体单元精确的处理能力和网格划分自适应技术也是其优势所在。
1 指数形与圆锥形变幅杆对比分析
　　超声变幅杆的性能可以用许多参量来描述。实际应用中常用共振频率（共振长度）、放大系数、形状因素、输入力阻抗和弯曲劲度等[8] 。
　　设计参数为：变幅杆选用的材料为45 号钢，声速c=5160m/s，变幅杆工作频率f=20kHz，变幅杆的大端直径D 1=52mm, 小端直径为D 2=16mm。根据常用变幅杆材料特性可知，材料密度ρ =7800kg/m3，弹性模量E=20800kg/mm2，泊松比为0.28。
   （1）指数形变幅杆动力学分析。
　　利用ANSYS 分析软件对指数形变幅杆进行建模并计算，力图直观准确地分析变幅杆的振动，对指数形变幅杆进行模态分析及谐响应分析，以验证理论设计的工作频率及所受的应力应变情况，并计算出放大系数与理论值进行比较。
　　在本文中，采用Solid95 单元作为基本的单元类型，能够用于不规则形状，而且不会在精度上有任何损失。该单元由20 个节点定义，每个节点3 个自由度：x，y，z 方向。
　　首先对变幅杆建模并进行网格划分，见图3。在模态分析[9] 之前，设置模态提取方法为Block Lanczos，待提取的模态

个数为7，频率范围控制在10~30kHz 之间。模态分析所得到的指数形变幅杆1~7 阶固有频率分别为14.265kHz、14.467kHz、14.471kHz、19.685kHz、24.342kHz、24.501kHz、24.510kHz。从固有频率中取与工作频率20kHz 最接近的频率，发现此变幅杆在19.685kHz 时发生纵振，此时其各点的位移矢量均沿轴向方向，由此可得指数形变幅杆的实际纵振频率为19.685kHz。在谐响应分析中，研究固有振动频率20kHz 附近的响应特性。加载时，在变幅杆大端yz 面内所有的节点上施加x 方向为 0.005mm 的位移，设定强制频率范围为14~28kHz。
　　指数形变幅杆在固有频率为19.685kHz 时，变幅杆大端输入振幅为5×10-6m，小端输出振幅为0.162×10-4m，振幅放大3.24 倍，如图4 所示。从图5 中可以看到位移节点位于大端56.1mm 处，从图6 中可以看到最大工作应力位于大端87mm 处。

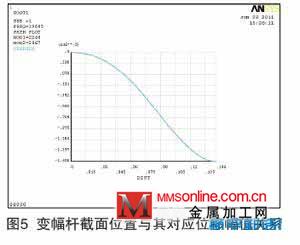
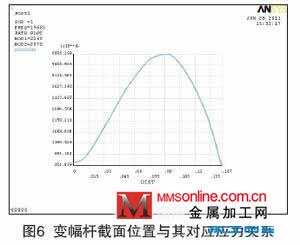
   （2）圆锥形变幅杆动力学分析。
　　首先进行模态分析，分析过程与上述分析指数形变幅杆方法相同。设置模态提取方法为Block Lanczos，则圆锥形变幅杆1~7 阶固有频率为14.705kHz、15.593kHz、15.6kHz、19.875kHz、24.670kHz、25.683kHz、25.702kHz。从固有频率中取与工作频率20kHz 最接近的频率，此时发现圆锥

　　形变幅杆在19.875kHz 时发生纵振，此时其各点的位移矢量均沿轴向方向，由此可得圆锥形变幅杆的实际纵振频率为19.875kHz。
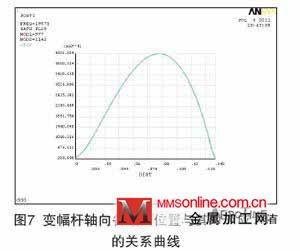
　　其次进行谐响应分析，分析过程与上述相同。固有频率为19.875kHz时圆锥形变幅杆轴向各截面位置与其对应应力值的关系曲线如图7 所示。从图中可以看到此时圆锥形变幅杆最大工作应力位于离大端88.4mm处。固有频率为19.875kHz 时圆锥形变幅杆的振型如图8 所示，根据计算得出圆锥形变幅杆放大倍数为2.8，位移节点位于离大端58.2mm 处。
2 指数形与圆锥形变幅杆对比
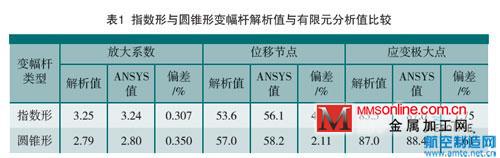
　　利用ANSYS 软件对两类变幅杆进行谐响应分析，所得结果见表1。

振动系统分析
　　首先，变幅杆要与传振杆相连接就需要在变幅杆大端设计螺栓头，因图3 指数形变幅杆网格划分示意图此在模型上安装螺栓头后对其进行模态分析，结果显示加螺栓头后的谐振频率与没加前相差无几，所以在一般情况下，设计变幅杆时可忽略其对变幅杆谐振频率的影响[10]。
　　其次，变幅杆前端还要安装工具头。对安装了工具头的变幅杆进行模态分析后得到变幅杆谐振频率为1.793kHz，和未加工具头时相比降低了1.759kHz，如图9 所示。此时可以通过削短变幅杆的方法来提高其固有频率，使变幅杆带工具头后

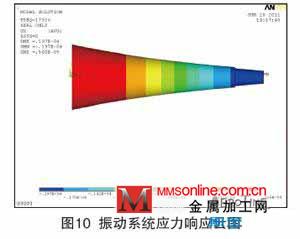
的振动频率提高到所要求的设计值，并借助有限元方法对变幅杆进行修正[11] 设计。图10 为变幅杆应力响应云图，从图中可得出最大响应应力为51.3MPa，远小于480MPa, 完全能够满足材料要求。
　　谐响应分析结果显示指数形变幅杆加工具头后在共振频率下的放大系数为3.94，圆锥形变幅杆加工具头在共振频率下的放大系数为3.01。这表明带工具后变幅杆放大系数比无工具时略有变大。
两种变幅杆的放大系数的比较试验
　　为了验证设计的变幅杆的放大系数，主要的试验装置有超声波发生器、圆锥形、指数形变幅杆、超声斩波器、电解电源、PC 机等。
　　试验步骤：首先，对圆锥形变幅杆的加工振幅进行试验，使系统处于共振状态，得到的振幅大约为0.0065mm ；同理，使用相同的方法，对指数形变幅杆的加工振幅进行实际测量，得到的振幅大约为0.0077mm。对试验结果进行分析，圆锥形与指数形的加工振幅之比为1∶1.18，由于加工功率是保持不变的，通过有限元动态仿真得到的比值为1∶1.16，验证了这两种类型的变幅杆之间的关系。
试验及分析
　　在实际加工中，指数形变幅杆放大系数稍大于圆锥形变幅杆。相同条件下，指数形变幅杆虽然加工效率一般，但加工谐振频带较宽，可以保证较长时间在接近恒定频率下工作，加工过程较为稳定。
　　主要试验设备及仪器有：精密超声加工机、 MC-6 型脉冲电源、电源斩波器、调制电路、限流电阻，体视显微镜、LDS21010 数字存储示波器双通道数字存储示波器、PC 机等。数字示波器采集的限流电阻两端的电压信号可表征超声电解复合加工的电流信号。
　　加工参数及材料有：微小内齿轮工具阴极（z=18， m=0.20mm），电解电压幅值3V，电解液为质量分数5% 的 NaNO3 水溶液，静压力2.0N，超声功率50W，B4C-W10 混粉， 加工时间2min，材料硬质合金（YBD151）。进行单一超声加工、超声直流电解复合加工对比试验。加工的微齿轮显微放大图如图11（a）、（b）所示，可以看出超声电解复合加工

得到的微齿轮加工效率（深度）高于单一超声加工。
结论
   （1）用ANSYS 方法分析得到的超声振动系统参数与试验测量结果基本一致。
   （2）优化设计的变幅杆与工具电极满足电解复合加工系统要求；采用指数形变幅杆，加工过程更稳定。
   （3）超声电解复合加工可得到更好的表面质量及加工精度，且加工效率更高。